题目
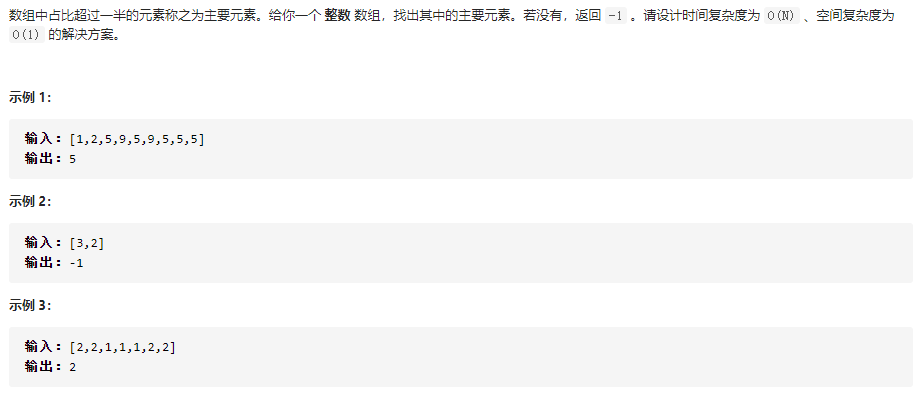
如果在不考虑时间复杂度和空间复杂度的情况下。可以先直接进行排序,然后循环一次进行判断是否为主要元素。
示例如下
1
2
3
4
5
6
7
8
9
10
11
12
13
| public int majorityElement(int[] nums) {
int len= nums.length /2;
Arrays.sort(nums);
int index =0;
while( index<=len){
if(nums[index]==nums[index+len]){
return nums[index];
}
index++;
}
return -1;
}
|
题目中对时间复杂度和空间复杂度是有要求的。时间复杂度为O(n)、空间复杂度为O(1)。所以上面的方法是达不到标准的。后面了解到了一个算法是符合要求,叫多数投票算法(摩尔投票算法)。
摩尔投票算法
关于摩尔投票算法的定义和伪代码就直接贴维基百科的解释了。
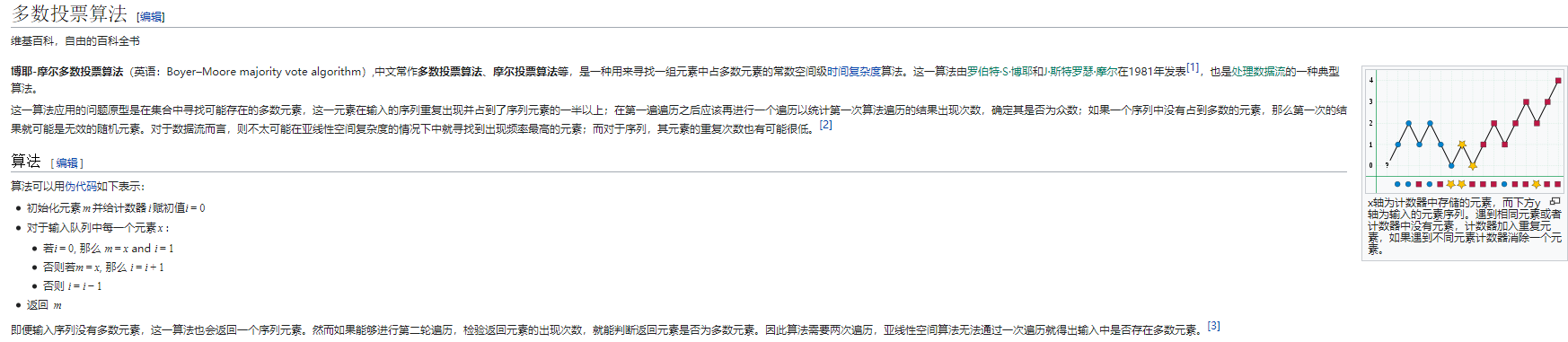
具体实现
第一版的实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| public class Solution {
public int MajorityElement(int[] nums) {
int major = -1, count = 0;
foreach (var num in nums)
{
if (count == 0)
major = num;
if (major == num)
{
count++;
}
else
{
count--;
}
}
count = 0;
foreach (var num in nums)
{
if (num == major)
{
count++;
}
}
if (count > nums.Count() / 2)
return major;
return -1;
}
}
|
这里的实现,对入参还是缺少一部分校验。以及部分可以返回的判断。比如nums的长度为1时,是可以直接返回的;nums是null时,可以直接返回-1等等。
补充了部分判断的实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| public int MajorityElement(int[] nums)
{
int major = -1, count = 0;
if(nums ==null)
{
return -1;
}
if(nums.Length ==1)
{
return nums[0];
}
foreach (var num in nums)
{
if (count == 0)
major = num;
if (major == num)
{
count++;
}
else
{
count--;
}
}
count = 0;
foreach (var num in nums)
{
if (num == major)
{
count++;
}
}
if (count > nums.Count() / 2)
return major;
return -1;
}
|
摩尔投票的变式
题目解析
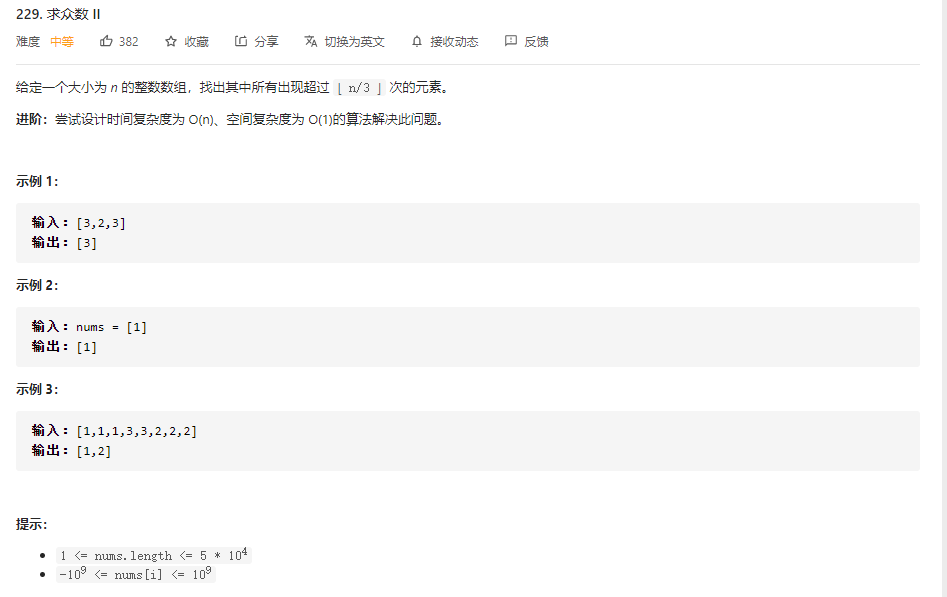
这道题目是要求找到数组中出现次数超过n/3次的元素。一样是可以通过摩尔投票算法去解决的。只是需要稍微改进一下。既然是要求出现次数超过n/3的元素才返回。推理一下就得到任何一个数组最多就只能返回两个数字。那就需要魔改一下摩尔投票的判断逻辑。
思路解析
初始化元素m,n并给它们对应的计数器i,j 赋初始值i=0,j=0
对于输入队列中每一个元素x:
- 若i=0 and j=0,那么m=x and i=1
- 否则若i=0 and j!=0 and n!=x,那么 m=x and i=1
- 否则若m=x,那么i=i+1
- 否则若j!=0 and n != x,那么 i=i-1 and j=j-1
- 否则若j=0,那么n= and j=1
- 否则若n=x,那么j=j+1
- 否则若i=0 and m!=x,那么j=j-1
返回m,n
循环判断m,n是否出现次数达到要求,达到则加入list,否则不加入
返回list
实现代码
调整后的实现代码如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
| public IList<int> MajorityElement(int[] nums)
{
var list = new List<int>();
if (nums.Length < 3)
{
list.AddRange(nums.Distinct());
return list;
}
int major1 = 0, major1count = 0, major2 = 0, major2count = 0;
for (int i = 0; i < nums.Length; i++)
{
if (major1count == 0 && major2count == 0)
{
major1 = nums[i];
major1count = 1;
}
else if (major1count == 0 && major2count > 0 && major2 != nums[i])
{
major1 = nums[i];
major1count = 1;
}
else if (major1 == nums[i])
{
major1count++;
}
else if (major2count != 0 && major2 != nums[i])
{
major1count--;
major2count--;
}
else if (major2count == 0)
{
major2 = nums[i];
major2count = 1;
}
else if (major2 == nums[i])
{
major2count++;
}
else if (major1count != 0 && major1 != nums[i])
{
major2count--;
}
}
int major1Count = 0, major2Count = 0;
for (int i = 0; i < nums.Length; i++)
{
if (nums[i] == major1)
major1Count++;
if (nums[i] == major2)
major2Count++;
if (major1Count == nums.Length)
{
if (!list.Contains(major1))
{
list.Add(major1);
return list;
}
}
if (major2Count == nums.Length)
{
if (!list.Contains(major1))
{
list.Add(major2);
return list;
}
}
if (major1Count > nums.Length / 3)
{
if (!list.Contains(major1))
{
list.Add(major1);
continue;
}
}
if (major2Count > nums.Length / 3)
{
if (!list.Contains(major2))
{
list.Add(major2);
continue;
}
}
}
return list;
}
|


